문제 정보
9095번: 1, 2, 3 더하기
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
www.acmicpc.net
핵심
1, 2, 3 총 3개의 정수로 0<n<11 인 정수를 표현하는 방법의 수를 출력하는 문제
처음에 해당 문제를 재귀호출을 이용해서 풀이하였지만, 더 좋은 방법인 DP를 활용할 수 있다는 사실을 알고
익힐만큼 공부하여 해당 문제와 개념부분을 정리해본다
풀이
기존 나의 풀이
import sys
input = sys.stdin.read
def recursive(remain):
if remain == 0:
global result
result += 1
elif remain < 0:
return
else:
recursive(remain-1)
recursive(remain-2)
recursive(remain-3)
N = list(map(int, input().split()[1:]))
for n in N:
result = 0
recursive(n)
print(result)첫번째 풀이, 정수 n을 인자로 주고, 여기에 1, 2, 3을 뺀 각각의 함수를 다시 재귀적으로 호출한다
계속 호출하다 보면, 모든 경우의 수가 나오고 remain이 0이 되면 result에 1을 더해주는 식으로 풀이를 진행하였다
해당 코드도 실행시간이 DP와 얼마 차이가 나지는 않지만, 이는 n의 범위가 10까지로, 작은 수이기 때문에 그런 것이고 더 많은 범위를 요하게 된다면 차이가 더 많이 날 것이다
DP를 활용한 풀이
import sys
input = sys.stdin.read
dp = [0] * 12
dp[1] = 1
dp[2] = 2
dp[3] = 4
N = list(map(int, input().split()[1:]))
for n in N:
for i in range(4, n+1):
if dp[i] != 0:
continue
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
print(dp[n])DP란 Dynamic Programming의 약자고 큰 문제를 작은 문제로 쪼개서 그 답을 저장해두고 재활용하는 알고리즘이다
일반적인 재귀호출의 경우, 같은 호출이 여러번 반복되게 되면 비효율적이기 때문에, 작은 문제부터 계산 결과값을 저장해 두고, 이를 재사용 하는 방법으로 풀이를 개선할 수 있다
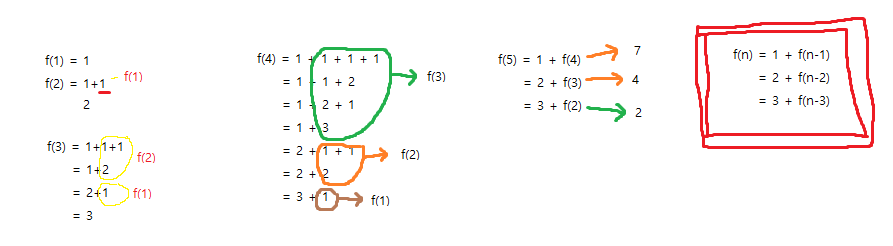
풀이과정을 보면 다음과 같은데, 조금만 나열해서 풀어 써보면 해당 관계를 찾을 수 있다
1, 2, 3 총 3가지 숫자를 통해 덧셈을 표현해야 하므로, 1을 먼저 더했을 때, 2를 먼저 더했을때와 3을 먼저 더했을 때 총 3가지 경우의 수로 일단 나눠지고
그 중에서 1을 더하면 f(n-1), 2를 더하면 f(n-2), 3을 더하면 f(n-3)의 세가지 경우로 나누어진다
그렇기에 예를 들어 f(5) = 1+f(4) 에서 f(4)가 얼마가 나오는지는 우리가 이전에 f(1), f(2), f(3)을 통한 f(4)의 계산에서 미리 알고 있기 때문에 그동안의 경험을 저장해놓고 이를 이용하여 구해낼 수 있다
이처럼 n의 수가 주어지더라도, 이전 계산을 통한 경험을 저장해 놓고 이를 활용한다면 쉽게 풀이할 수 있다
고찰
DP 알고리즘에 대해 간단히 정리해보고자 한다
크게 우리가 DP는 피보나치같이, 큰 문제들을 작은 문제들로 분할하였을 때 동일 부분의 문제가 중복되어 나타날 때 사용할 수 있다.
이를 Overlapping Subproblems 라고 한다.
또한 부분 문제에서 최적 결과의 값을 사용하여 전체 문제의 최적 결과를 낼 수 있는 경우를 의미한다
우리가 피보나치의 경우와 이전 문제의 경우에서도 미리 계산한 계산값을 그대로 사용하여 전체 답을 구할 수 있으므로 최적 부분 구조를 가지고 말할 수 있다
이를 Optimal Substructrue 이라고 한다.
위 두가지 조건을 만족한다면 DP를 구현할 수 있는데, 관계식을 만들고 변수의 값에 따른 결과를 저장하며 구현의 과정을 거치면 된다
이 이상의 설명은 사실 다른분이 더 상세한 설명을 제공하는 것 같아 아래 링크에 참고자료를 남겨두도록 하겠다
참고
GitHub - dduneon/CodingTestPy
Contribute to dduneon/CodingTestPy development by creating an account on GitHub.
github.com
알고리즘 - Dynamic Programming(동적 계획법)
1. 개요 DP, 즉 다이나믹 프로그래밍(또는 동적 계획법)은 기본적인 아이디어로 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것으로
hongjw1938.tistory.com


댓글